Kent distribution

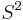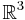The 5-parameter Fisher-Bingham distribution or Kent distribution, named after Ronald Fisher, Christopher Bingham, and John T. Kent, is a probability distribution on the two-dimensional unit sphere S^{2}\, in \Bbb{R}^{3} . It is the analogue on the two-dimensional unit sphere of the bivariate normal distribution with an unconstrained covariance matrix. The distribution belongs to the field of directional statistics. The Kent distribution was proposed by John T. Kent in 1982, and is used in geology and bioinformatics.

The probability density function 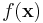f(\mathbf{x})\, of the Kent distribution is given by:

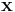f(\mathbf{x})=\frac{1}{\textrm{c}(\kappa,\beta)}\exp\{\kappa\boldsymbol{\gamma}_{1}\cdot\mathbf{x}%2B\beta[(\boldsymbol{\gamma}_{2}\cdot\mathbf{x})^{2}-(\boldsymbol{\gamma}_{3}\cdot\mathbf{x})^{2}]\}

where \mathbf{x}\, is a three-dimensional unit vector and 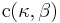\textrm{c}(\kappa,\beta)\, is a normalizing constant.

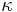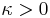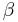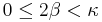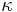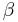The parameter \kappa\, (with \kappa>0\, ) determines the concentration or spread of the distribution, while \beta\, (with 0\leq2\beta<\kappa ) determines the ellipticity of the contours of equal probability. The higher the \kappa\, and \beta\, parameters, the more concentrated and elliptical the distribution will be, respectively. Vector 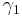\gamma_{1}\, is the mean direction, and vectors 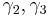\gamma_{2},\gamma_{3}\, are the major and minor axes. The latter two vectors determine the orientation of the equal probability contours on the sphere, while the first vector determines the common center of the contours. The 3x3 matrix 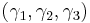(\gamma_{1},\gamma_{2},\gamma_{3})\, must be orthogonal.

See also

References
 
Univariate (circular) directional: Circular uniform · univariate von Mises · wrapped normal  · wrapped Cauchy  · wrapped exponential  · wrapped Lévy
Bivariate (spherical): Kent       Bivariate (toroidal): bivariate von Mises
Multivariate: von Mises–Fisher  · Bingham